Applications of Gauss Law
Applications of Gauss Law
Electric field due to an infinitely long straight charged wire:
Consider a thin infinitely long straight wire having a uniform linear charge density λCm-1. By symmetry, the field E of the line charge is directed radialy outwards and its magnitude is same at all points equidistant from the line charge. To determine the field at a distance r from the line charge, we choose a cylindrical Gaussian surface of radius t and length I and with its axis along the line charge. As shown in fig. it has curved surface S1 and flat circular ends S2 and S3.
Obviously ds1 ||E, ds2 perpendicular E and ds3 perpendicular E . So only the curved surface contributes towards the total flux
= E * area of the curved surface
change enclosed by the Gaussian surface
q= λL
using enclosed by the Gaussian surface,
Thus the electric field of a line charge is inversely proportional to the distance from the line charges.
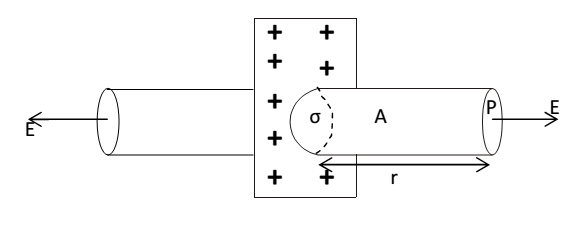
Electric field due to uniformly charged infinite plane sheet :
As shown in fog. Consider a thin, infinite plane sheet of charge with uniform surface charge density σ. We find out the electric field at point P at distance r from it.
As the lines of force are parallel to the curved surface of the cylinder, the flux through the curved surface is zero. The flux through the plane end faces of the cylinder is
ɸE = EA + EA = 2EA
charge enclosed by the Gaussian surface is
q = σ A
according to Gauss’s theorem
ɸE = q/ɛ0
The field points normally away from the plane sheet on its both sides if σ > 0 and into the plane sheet if σ < 0.
Electric field due to uniformly charged thin spherical shell:
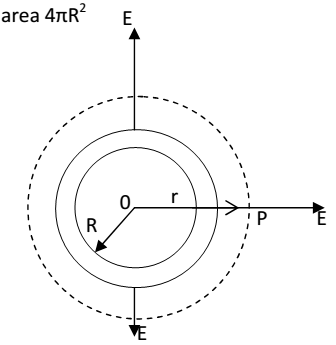
Consider thin spherical shell of charge of radius R with uniform surface charge density σ. From symmetry, we see that electric field E at any point is radial and had same magnitude at points equidistant from the centre of the shell. i.e. the field is spherically symmetric. To determine electric field at any point p at a distance r from o, we choose a concentric sphere of radius r as the Gaussian surface.
- When point p lies outside the spherical shell : The total charge q inside the Gaussian surface is the charge q on the shell of radius R and area 4πR2.Therefore q = 4 πR2 σ
Flux through the Gaussian surface,
ФE = E * 4πr2
Therefore,
Therefore,
This field is same as that produced by a charge q placed at the centre o. hence for points outside the shell, the field due to a uniformly charged shell is as if the entire charge of the shell is concentrated at its centre.
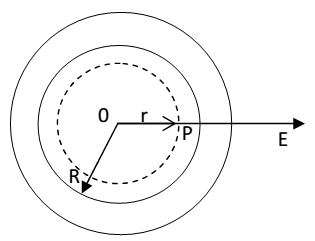
b) When point P lies on the spherical shell : the Gaussian surface just encloses the charged spherical shell.
Using Gauss theorem,
c) When point p lies inside the spherical shell: as is form fig. the charge enclosed by the Gaussian surface is zero, i.e. q=0
Flux through the Gaussian surface,
фE = E * 4πr2
Using Gauss theorem,
E * 4πr2 = 0
Or
E = 0
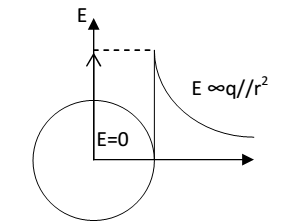
Hence electric field due to a uniformly charged spherical shell is zero at all points inside the shell. Fig. shows how E varies with distance r from the center of the shell of radius r. e is zero from r=0 to r=R, and beyond r= R, we have E α 1//r2 .
 SureDen
SureDen