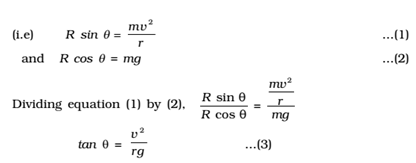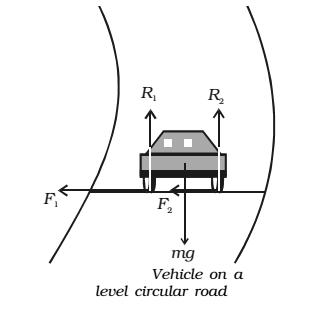
Motion on a level circular road

 

When a vehicle goes round a level curved path, it should be acted upon by a centripetal force. While negotiating the curved path, the wheels of the car have a tendency to leave the curved path and regain the straight-line path. Frictional force between the tyres and the road opposes this tendency of the wheels. This frictional force, therefore, acts towards the centre of the circular path and provides the necessary centripetal force.

R₁ + R₂ = mg                        ………..             (1)

F₁ and F₂ be the forces of friction between the tyres and the road, directed towards the centre of the curved path. ∴ F₁ = µR₁ and F₂ = µR                               ……..(2)

If v is velocity of the vehicle while negotiating the curve, the centripetal force required =mv² /r

As this force is provided only by the force of friction.

∴mv²/r   ≤ (  F₁+F₂)

             ≤ (µ R₁ + µR₂)

            ≤ µ (R₁ + R₂)

∴ mv²/r  ≤ µ mg (∵ R₁  + R2 = mg )

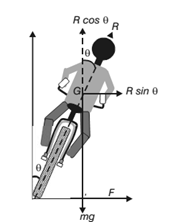
Bending of a cyclist round a curve

A cyclist has to bend slightly towards the centre of the circular track in order to take a safe turn without slipping.

Let m be the mass of the cyclist along with the bicycle and v, the velocity. When the cyclist negotiates the curve, he bends inwards from the vertical, by an angle θ. Let R be the reaction of the ground on the cyclist. The reaction R may be resolved into two components:

(i) the component R sin θ, acting towards the centre of the curve providing necessary centripetal force for circular motion and

(ii) the component R cos θ, balancing the weight of the cyclist along with the bicycle.

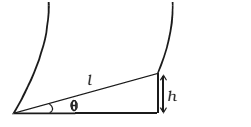
Thus for less bending of cyclist (i.e for θ to be small), the velocity v should be smaller and radius r should be larger. let h be the elevation of the outer edge of the road above the inner edge and l be the width of the road then,

sin θ = h/l ...(4)

For small values of θ, sin θ = tan θ

Therefore from equations (3) and (4)

tan θ =h/l = v²/ rg

Condition for skidding

When the centripetal force is greater than the frictional force, skidding occurs. If µ is the coefficient of friction between the road and  tyre, then the limiting friction (frictional force) is f = µR where normal reaction R = mg
∴ f = µ (mg)

Thus for skidding,

Centripetal force > Frictional force

mv²/ r > µ (mg)
But
v²/ rg = tan θ
∴ tan θ > µ
(i.e) when the tangent of the angle of banking is greater than the
coefficient of friction, skidding occurs.