Electric flux :

The electric flux through a given area held inside an electric field is the measure of the total number of electric lines of force passing normally through that area. As shown in fig. if an electric field E passes normally through an area element Δ S, then the electric flux through this area is

Δφ_E = E ΔS

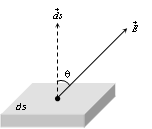
As shown in fig. if the normal drawn to the area element ΔS makes an angle θ with the uniform electric field E, then the component of  E normal to ΔS will be E cos θ, so the electric flux is

Δφ_E = E cosθ * ΔS

Electric flux is a scalar quantity.

Unit of electric flux is = unit of E *unit of Surface area

=NC^-1 m² = Nm²C^-1

S.I. unit of electric flux

Vm^-1*m² = Vm

Gauss theorem :

It states that the total flux through a closed surface is 1/ε₀ times the net charge enclosed by the closed surface.

Mathematically, it can be xepressed as

Proof: consider an isolated point charge q as shown in fig. suppose the surface S is a sphere of radius r centered on q. then surface S is a Gaussian surface. Electric field at any point S is

this field point radialy outward at all points on S. also, any area element points radially outwards, so it is parallel to E.

i.e. θ = 0       

=E * total area of sphere  = 

this proves the Gauss’s theorem.