Exercise – 2.2

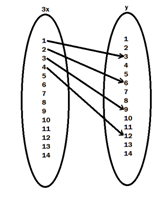
1. Let A = {1, 2, 3, ……, 14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, where x, y Є A}. Write its domain, Co domain and range.

3x – y = 0

3x = y

(i) R = {(x, y) : 3x – y = 0, where x, y Є A} = {(1, 3), (2, 6), (3, 9), (4, 12)}

(ii) Domain = {1, 2, 3, 4, 5,.…… 14}

(iii) Co domain = {1, 2, 3, 4, 5, ….. 4}

(iv) Range = {3, 6, 9, 12}

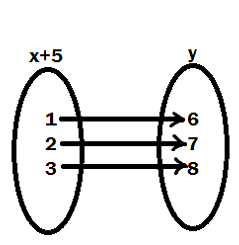
2. Define a relation R on the set N of natural numbers by R = {(x, y) : y = x + 5, x is a natural no. less than 4; x, y Є N}. Depict the relationship using roster form write down the domain & the range.

(i) R = {(1, 6), (2, 7), (3, 8)}

(ii) Domain = {1, 2, 3}

(iii) Range = {6, 7, 8}

3. A = {1, 2, 3, 5} and = {4, 6, 9}. Define a relation R from A to B by R = {(x, y): the difference b/w x & y is odd ; x Є A, y Є B}. Write r in roster form

R = {(1, 4), (1, 6), (2, 9), (3, 4), (3, 6), (5, 4), (5, 6)}

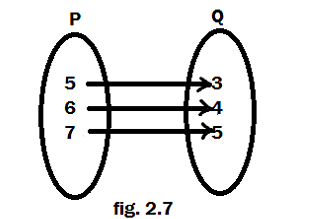
4. The fig 2.7 shows a relationship b/w the sets P & Q. write this relation

(i) in set builder form.                          

(ii) in roster form.

write its Domain  & Range?

Sol:- (i) {x : x = y + 2}

(iii) R = {(5, 3), (6, 4), (7, 5)}

Domain = {5, 6, 7}, Range = {3, 4, 5}

5. Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by {(a, b)} : a, b Є A, b is exactly divisible by A}

(i) Write R in roster form

(ii) Find the domain of r

(iii) Find the range of R

Sol:- (i) R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 4), (2, 6), (3, 6), (2, 2), (3, 3), (4, 4), (6, 6)}

(ii) Domain = {1, 2, 3, 4, 6}

(iii) Range = {1, 2, 3, 4, 6}

6. Determine the domain and the range of the relation R defined by R = {x, x + 5) : x Є {0, 1, 2, 3, 4, 5}}

Domain = {0, 1, 2, 3, 4, 5},        Range = {5, 6, 7, 8, 9, 10}

7. Write the relation R = {(x, x³) : x is a prime no less than 10} in roster form.

Prime number less than 10 = (2, 3, 5, 7)

∴ R = {(2, 8), (3, 27), (5, 125), (7, 343)}

8. Let A = {x, y, z} and B = {1, 2}. Find the no. of relations from A to B

By using formula,

No. of relations = 2mn

= 2^{3 x 2} = 2⁶

9. Let R be the relation on Z defined by R = {(a, b) : a, b Є Z, a – b is an integer}. Find the domain and the range of R.

Domain = Z (Integers)

Range = Z (Integers)